Toric code
The Toric Code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two dimensional spin lattice [1] It is the simplest and most well studied of the quantum double models. [2]
Contents |
Error correction and computation
The toric code is defined on a two dimensional lattice, usually chosen to be the square lattice, with a spin-½ particle located on each edge. The periodic boundary conditions of the lattice are chosen such that it is wrapped around a torus, giving the code its name. Stabilizer operators are defined on the spins around each vertex  and plaquette (or face)
and plaquette (or face)  of the lattice as follows,
of the lattice as follows,
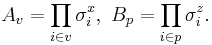
Where here we use 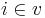 to denote the edges touching the vertex
to denote the edges touching the vertex  , and
, and 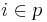 to denote the edges surrounding the plaquette
to denote the edges surrounding the plaquette  . The stabilizer space of the code is that for which all stabilizers act trivially, hence,
. The stabilizer space of the code is that for which all stabilizers act trivially, hence,
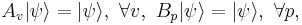
for any state 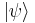 . For the toric code, this space is four dimensional, and so can be used to store two qubits of quantum information. This can be proven by considering the number of independent stabilizer operators. The occurrence of errors will move the state out of the stabilizer space, resulting in vertices and plaquettes for which the above condition does not hold. The positions of these violations is the syndrome of the code, which can be used for error correction.
. For the toric code, this space is four dimensional, and so can be used to store two qubits of quantum information. This can be proven by considering the number of independent stabilizer operators. The occurrence of errors will move the state out of the stabilizer space, resulting in vertices and plaquettes for which the above condition does not hold. The positions of these violations is the syndrome of the code, which can be used for error correction.
The unique nature of the topological codes, such as the toric code, is that stabilizer violations can be interpreted as quasiparticles. Specifically, if the code is in a state 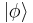 such that,
such that,
 ,
,
a quasiparticle known as an  anyon can be said to exist on the vertex
anyon can be said to exist on the vertex  . Similarly violations of the
. Similarly violations of the 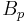 are associated with so called
are associated with so called  anyons on the plaquettes. The stabilizer space therefore corresponds to the anyonic vacuum. Single spin errors cause pairs of anyons to be created and transported around the lattice.
anyons on the plaquettes. The stabilizer space therefore corresponds to the anyonic vacuum. Single spin errors cause pairs of anyons to be created and transported around the lattice.
When errors create an anyon pair and move the anyons, one can imagine a path connecting the two composed of all links acted upon. If the anyons then meet and are annihilated, this path describes a loop. If the loop is topologically trivial, it has no effect on the stored information. The annihilation of the anyons in this case corrects all of the errors involved in their creation and transport. However, if the loop is topologically non-trivial, though reannihilation of the anyons returns the state to the stabilizer space it also implements a logical operation on the stored information. The errors in this case are therefore not corrected, but consolidated.
Let us use  to denote the probability of a
to denote the probability of a 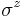 error on each spin. When
error on each spin. When  is low, this will create sparsely distributed pairs of
is low, this will create sparsely distributed pairs of  anyons which have not moved far from their point of creation. In this case minimum weight perfect matching can be used to identify the pairs and reannihilate them, correcting the errors [3]. As
anyons which have not moved far from their point of creation. In this case minimum weight perfect matching can be used to identify the pairs and reannihilate them, correcting the errors [3]. As  increases, however, it becomes more ambiguous as to how the anyons may be matched without risking the formation of topologically non-trivial loops. This gives a threshold probability, under which the error correction will almost certainly succeed. Through a mapping to the random bond Ising model, this critical probability has been found to be
increases, however, it becomes more ambiguous as to how the anyons may be matched without risking the formation of topologically non-trivial loops. This gives a threshold probability, under which the error correction will almost certainly succeed. Through a mapping to the random bond Ising model, this critical probability has been found to be 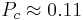 .[4] The threshold holds also for
.[4] The threshold holds also for 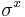 errors.
errors.
The means to perform quantum computation on logical information stored within the toric code has been considered, with the properties of the code providing fault-tolerance. It has been shown that extending the stabilizer space using 'holes', vertices or plaquettes on which stabilizers are not enforced, allows a universal set of gates to be performed. A measurement based scheme for quantum computation based upon this principle has been found, whose error threshold is the highest known for a two dimensional architecture.[5]
Hamiltonian
Since the stabilizer operators of the toric code are quasilocal, acting only on spins located near each other on a two dimensional lattice, it is not unrealistic to define the following Hamiltonian,
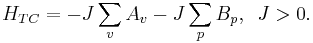
The ground state of this Hamiltonian is the stabilizer space of the code. Excited states correspond to those of anyons, with the energy proportional to their number. Local errors are therefore energetically suppressed by the gap, which has been shown to be stable against local perturbations.[6] However, the dynamic effects of such perturbations can still cause problems for the code.[7]
The gap also gives the code a certain resilience against thermal errors, allowing it to be correctable almost surely for a certain critical time. This time increases with  , but since arbitrary increases of this coupling are unrealistic, the code still has its limits. Accordingly, many attempts are being made to make the toric code fully thermally stable with a lifetime which increases with the system size [8][9].
, but since arbitrary increases of this coupling are unrealistic, the code still has its limits. Accordingly, many attempts are being made to make the toric code fully thermally stable with a lifetime which increases with the system size [8][9].
Anyon model
As mention above, so called  and
and  quasiparticles are associated with the vertices and plaquettes of the model, respectively. These quasiparticles can be described as anyons, due to the non-trivial effect of their braiding. Specifically, though both species of anyons are bosonic with respect to themselves, the braiding of two
quasiparticles are associated with the vertices and plaquettes of the model, respectively. These quasiparticles can be described as anyons, due to the non-trivial effect of their braiding. Specifically, though both species of anyons are bosonic with respect to themselves, the braiding of two  's or
's or  's having no effect, a full monodromy of an
's having no effect, a full monodromy of an  and an
and an  will yield a phase of
will yield a phase of 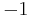 . Such a result is not consistent with either bosonic or fermionic statistics, and hence is anyonic.
. Such a result is not consistent with either bosonic or fermionic statistics, and hence is anyonic.
The anyonic mutual statistics of the quasiparticles demonstrate the logical operations performed by topologically non-trivial loops. Consider the creation of a pair of  anyons followed by the transport of one around a topologically nontrivial loop, such as that shown on the torus in blue on the figure above, before the pair are reannhilated. The state is returned to the stabilizer space, but the loop implements a logical operation on one of the stored qubits. If
anyons followed by the transport of one around a topologically nontrivial loop, such as that shown on the torus in blue on the figure above, before the pair are reannhilated. The state is returned to the stabilizer space, but the loop implements a logical operation on one of the stored qubits. If  anyons are similarly moved through the red loop above a logical operation will also result. The phase of
anyons are similarly moved through the red loop above a logical operation will also result. The phase of 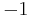 resulting when braiding the anyons shows that these operations do not commute, but rather anticommute. They may therefore be interpreted as logical
resulting when braiding the anyons shows that these operations do not commute, but rather anticommute. They may therefore be interpreted as logical  and
and  Pauli operators on one of the stored qubits. The corresponding logical Pauli's on the other qubit correspond to an
Pauli operators on one of the stored qubits. The corresponding logical Pauli's on the other qubit correspond to an  anyon following the blue loop and an
anyon following the blue loop and an  anyon following the red. No braiding occurs when
anyon following the red. No braiding occurs when  and
and  pass through parallel paths, the phase of
pass through parallel paths, the phase of 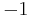 therefore does not arise and the corresponding logical operations commute. This is as should be expected since these form operations acting on different qubits.
therefore does not arise and the corresponding logical operations commute. This is as should be expected since these form operations acting on different qubits.
Due to the fact that both  and
and  anyons can be created in pairs, it is clear to see that both these quasiparticles are their own antiparticles. A composite particle composed of two
anyons can be created in pairs, it is clear to see that both these quasiparticles are their own antiparticles. A composite particle composed of two  anyons is therefore equivalent to the vacuum, since the vacuum can yield such a pair and such a pair will annihilate to the vacuum. Accordingly, these composites have bosonic statistics, since their braiding is always completely trivial. A composite of two
anyons is therefore equivalent to the vacuum, since the vacuum can yield such a pair and such a pair will annihilate to the vacuum. Accordingly, these composites have bosonic statistics, since their braiding is always completely trivial. A composite of two  anyons is similarly equivalent to the vacuum. The creation of such composites is known as the fusion of anyons, and the results can be written in terms of fusion rules. In this case, these take the form,
anyons is similarly equivalent to the vacuum. The creation of such composites is known as the fusion of anyons, and the results can be written in terms of fusion rules. In this case, these take the form,
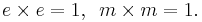
Where 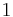 denotes the vacuum. A composite of an
denotes the vacuum. A composite of an  and an
and an  is not trivial. This therefore constitutes another quasiparticle in the model, sometimes denoted
is not trivial. This therefore constitutes another quasiparticle in the model, sometimes denoted  , with fusion rule,
, with fusion rule,
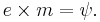
From the braiding statistics of the anyons we see that, since any single exchange of two  's will involve a full monodromy of a constituent
's will involve a full monodromy of a constituent  and
and  , a phase of
, a phase of 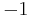 will result. This implies fermionic self-statistics for the
will result. This implies fermionic self-statistics for the  's.
's.
Other uses
As a simple model of anyons, the toric code can be used in studies of anyonic behaviour and topologically ordered systems. For example, it has been used to study the effects of thermalization on the topological entropy of states.[10] It has also been shown that, using superposition states of the Abelian toric code anyons, some properties of the more complex non-Abelian anyons can be realized.[11]
Generalizations
The use of a torus is not required to form an error correcting code. Other surfaces may also be used, with their topological properties determining the degeneracy of the stabilizer space. In general, quantum error correcting codes defined on two dimensional spin lattices according to the principles above are known as surface codes.
It is also possible to define similar codes using higher dimensional spins.[12] These are the quantum double models, which allow a greater richness in the behaviour of anyons, and so may be used for more advanced quantum computation and error correction proposals.[13] These not only include models with Abelian anyons, but also those with non-Abelian statistics.[14]
Experimental Progress
The most explicit demonstration of the properties of the toric code has been in state based approaches. Rather than attempting to realize the Hamiltonian, these simply prepare the code in the stabilizer space and demonstrate the creation, transport and statistics of the anyons. [15]
For realizations of the toric code and its generalizations with a Hamiltonian, much progress has been made using Josephson junctions. The theory of how the Hamiltonians may be implemented has been developed for a wide class of topological codes. [16] An experiment has also been performed, realizing the toric code Hamiltonian for a small lattice, and demonstrating the quantum memory provided by its degenerate ground state. [17]
Other theoretical work towards experimental realizations is based on cold atoms. A toolkit of methods that may be used to realize topological codes with optical lattices has been explored, [18] as have experiments concerning minimal instances of topological order. [19] Progress is also being made into simulations of the toric model with Rydberg atoms, in which the Hamiltonian and the effects of dissipative noise can be demonstrated. [20]
References
- ^ A. Y. Kitaev, Proceedings of the 3rd International Conference of Quantum Communication and Measurement, Ed. O. Hirota, A. S. Holevo, and C. M. Caves (New York, Plenum, 1997).
- ^ A. Kitaev, Ann. Phys. 321, 2 (2006).
- ^ Edmonds, Jack (1965). "Paths, trees, and flowers". Canad. J. Math. 17: 449–467.
- ^ E. Dennis, A. Kitaev, A. Landahl, J. Preskill, J. Math. Phys. 43, 4452 (2002).
- ^ R. Raussendorf, J. Harrington, Phys. Rev. Lett. 98, 190504 (2007); R. Raussendorf, J. Harrington and K. Goyal, New J. Phys. 9, 199, (2007).
- ^ S. Bravyi, M. Hastings and S. Michalakis, J. Math. Phys. 51, 093512 (2010)
- ^ F. Pastawski, A. Kay, N. Schuch, I. Cirac, arXiv:0911.3843 (2009).
- ^ A. Hamma, C. Castelnovo, C. Chamon, Phys. Rev. B 79, 245122 (2009).
- ^ S. Chesi, B. Rothlisberger, D. Loss, Phys. Rev. A 82, 022305 (2010).
- ^ S. Iblisdir, D. Perez-Garcia, M. Aguado and J. Pachos, Phys. Rev. B 79, 134303 (2009).
- ^ J. R. Wootton, V. Lahtinen, Z. Wang and J. K. Pachos, Phys. Rev. B 78, 161102(R) (2008).
- ^ S. S. Bullock and G. K. Brennen, J. Phys. A 40, 3481-3505 (2007).
- ^ J. R. Wootton, V. Lahtinen, B. Doucot and J. K. Pachos, arXiv:0908.0708 (2009).
- ^ M. Aguado, G. K. Brennen, F. Verstraete and J. I. Cirac, Rev. Lett. 101, 260501 (2008); G. K. Brennen, M. Aguado, and J. I. Cirac, New J. Phys. 11, 053009 (2009).
- ^ J. K. Pachos, W. Wieczorek, C. Schmid, N. Kiesel, R. Pohlner, H. Weinfurter, New J. Phys. 11, 083010 (2009); C.-Y. Lu, W.-B. Gao, O. Gühne, X.-Q. Zhou, Z.-B. Chen, J.-W. Pan, Phys. Rev. Lett. 102, 030502 (2009).
- ^ B. Doucot, L. B. Ioffe and J. Vidal, Phys. Rev. B 69, 214501 (2004).
- ^ S. Gladchenko, D. Olaya, E. Dupont-Ferrier, B. Doucot, L. B. Ioffe, M. E. Gershenson, Nat. Phys. 5, 48 - 53 (2009).
- ^ A. Micheli, G. K. Brennen and P. Zoller, Nat. Phys. 2, 341 - 347 (2006).
- ^ B. Paredes and I. Bloch, Phys. Rev. A, 77, 023603 (2008).
- ^ H, Weimer, M. Müller, I. Lesanovsky, P. Zoller and H. P. Büchler, Nat. Phys. 6, 382 - 388 (2010).